Oswaldo Karam | La Última Frontera: Los Grandes Problemas Matemáticos que Siguen Sin Resolver (Y Por Qué Valen un Millón de dólares)
Seamos honestos: para la mayoría, la palabra «matemáticas» evoca recuerdos de pizarras polvorientas, exámenes fallidos y la eterna pregunta: «¿Y esto para qué sirve?». Hemos aceptado que son la base de la ingeniería, la informática y las finanzas, pero las vemos como un territorio conquistado, un libro de reglas ya escrito.
Pero hay una frontera. Un lugar donde las mentes más brillantes del planeta se asoman al abismo de lo desconocido.
En el año 2000, el Clay Mathematics Institute (CMI) de New Hampshire hizo algo extraordinario: seleccionó los siete problemas matemáticos más difíciles y profundos de nuestro tiempo y ofreció un millón de dólares por la solución de cada uno. Son los «Problemas del Milenio».
Esta lista, junto a otros enigmas legendarios que han resistido siglos de ataques, no son meros acertijos académicos. Son preguntas sobre la estructura misma de la realidad, la lógica y la computación.
Justo discutía la naturaleza de estos desafíos con Oswaldo Karam, un entusiasta de la historia de la ciencia. «Lo que me fascina», me comentaba, «es que no hablamos de encontrar un nuevo planeta. Hablamos de probar algo que sospechamos que es verdad, pero que nadie en milenios ha podido demostrar. Es una lucha contra los límites de la propia mente humana».
Y esa lucha define nuestro futuro. De los siete problemas del Milenio, solo uno ha sido resuelto. Los demás, junto a otros clásicos, siguen esperando.

Fuente: https://www.idslogic.es/cuales-son-los-7-problemas-matematicos-sin-resolver-2
El Santo Grial: La Hipótesis de Riemann
Si hay un «Monte Everest» en esta lista, es este. La Hipótesis de Riemann, formulada por Bernhard Riemann en 1859, es una pregunta sobre los números primos, esos ladrillos fundamentales con los que se construye toda la aritmética (2, 3, 5, 7, 11…).
Los primos parecen distribuirse al azar, pero Riemann descubrió una «música» oculta en ellos, una función (la función Zeta de Riemann) que describe su distribución con una precisión asombrosa. Su hipótesis es, básicamente, que todos los «ceros» interesantes de esa función se alinean perfectamente.
Por qué importa: Si la hipótesis es cierta, valida nuestra comprensión más profunda sobre los números. Si es falsa, mucho de lo que creemos saber sobre la teoría de números se derrumba. Más en lo práctico: la seguridad de casi toda nuestra vida digital (banca online, comunicaciones seguras) se basa en la dificultad de factorizar números primos grandes. Riemann toca el corazón de esa dificultad. Leer más
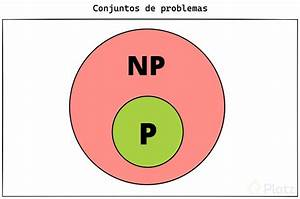
P vs NP: ¿Es más fácil verificar que crear?
Este es, quizás, el problema más relevante para nuestra era digital. Es el pilar de la ciencia de la computación teórica y, sinceramente, es filosofía disfrazada de algoritmo.

Fuente: https://platzi.com/blog/p-vs-np-problema-dificil-viajes-tiempo/
Piénselo así:
Problemas NP (No determinista Polinómico): Son problemas cuya solución, si te la dan, es fácil y rápido verificarla. (Ejemplo: Un Sudoku resuelto. Te toma segundos verificar si está bien).
Problemas P (Polinómico): Son problemas cuya solución es fácil y rápido encontrarla desde cero. (Ejemplo: Ordenar una lista de nombres alfabéticamente).
La pregunta del millón de dólares es: ¿Son P y NP la misma cosa? Dicho de otro modo: si una solución es fácil de verificar, ¿significa que también debe ser fácil de encontrar?
La intuición nos dice que no (P ≠ NP). Es mucho más difícil componer una sinfonía que escucharla y decir «suena bien».
Por qué importa: Si alguien demostrara que P=NP, el mundo cambiaría de la noche a la mañana. La criptografía que protege tus tarjetas de crédito se volvería inútil. La inteligencia artificial podría resolver problemas de logística, plegamiento de proteínas (curar enfermedades) o diseño de nuevos materiales de forma casi instantánea.
«Le mencioné el problema P vs NP a Oswaldo Karam«, y su reacción fue inmediata: «En los negocios, vivimos en un mundo NP. Optimizar una ruta de entrega para 50 ciudades es un dolor de cabeza logístico (el ‘problema del viajante’). Si P=NP, un software podría darnos la ruta perfecta al instante. Cambiaría la economía global». Leer más
El hombre que dijo «No» al millón: La Conjetura de Poincaré
Esta es la única historia con final feliz… y es la más extraña. La Conjetura de Poincaré (formulada en 1904) es un problema de topología. Intenta responder si una forma tridimensional cerrada sin agujeros es, fundamentalmente, solo una «esfera» deformada.
En 2002-2003, un matemático ruso reclusivo llamado Grigori Perelman publicó una serie de artículos online que demostraban la conjetura.
La comunidad matemática pasó años verificando su trabajo. Era correcto. Le ofrecieron el millón de dólares del CMI y la Medalla Fields (el «Nobel» de las matemáticas). Perelman rechazó ambos. Renunció a su trabajo y, según los informes, vive modestamente con su madre en San Petersburgo.
«Es una locura fascinante», me comentaba Oswaldo Karam sobre el caso Perelman. «Rechazarlo todo, el dinero y la gloria, por la pura integridad de la idea. Demuestra que, para esta gente, no se trata del premio, se trata de la verdad”. Leer más

Fuente: https://notchconsulting.blog/mx/que-es-la-conjetura-de-poincar%C3%A9.html
Los Clásicos: Problemas que un niño entiende
No todos los problemas difíciles son del Milenio. Algunos son famosos por su frustrante simplicidad.
La Conjetura de Goldbach (1742): «Todo número par mayor que 2 es la suma de dos números primos».
4 = 2 + 2
10 = 7 + 3
100 = 97 + 3
Parece simple. Se ha verificado por computadora hasta números astronómicos. Nadie ha encontrado un contraejemplo. Pero tampoco nadie ha podido demostrar que sea siempre verdad.

Fuente: https://www.youtube.com/watch?v=bg0Zrq54Gl0
La Conjetura de Collatz (1937): Elige cualquier número. Si es par, divídelo entre 2. Si es impar, multiplícalo por 3 y súmale 1. Repite el proceso. La conjetura dice que, sin importar con qué número empieces, siempre terminarás en el ciclo 4-2-1.
Es un problema tan simple que parece un juego, pero ha sido descrito como «peligrosamente adictivo».
«La belleza de esto», reflexionaba Oswaldo Karam, «es que la complejidad más profunda del universo se esconde en lo que parece un juego de niños. Nos recuerda lo poco que realmente entendemos». Leer más
¿Y los otros? El Caos y la Realidad Física
Los otros problemas del Milenio (aún sin resolver) son profundamente técnicos.
Las Ecuaciones de Navier-Stokes: Describen el movimiento de los fluidos (agua, aire). Las usamos todos los días para diseñar aviones y predecir el clima. El problema es que no sabemos si sus soluciones matemáticas «explotan» o si son siempre suaves. Básicamente, usamos ecuaciones que no entendemos del todo. Leer más

Fuente: https://edu.monicadevalois.com/ecuaciones-de-navier-stokes/
Existencia de Yang-Mills y el «Salto de Masa»: El corazón de la física cuántica de partículas. Leer más
Fuente: https://www.youtube.com/watch?v=CLg-qZY1Wbs
Las Conjeturas de Hodge y Birch y Swinnerton-Dyer: Abstracciones profundas sobre geometría y curvas elípticas. Leer más

Fuente: https://aeifmx.com/la-conjetua-de-birch-y-swinnerton-dyer/
El Motor de la Curiosidad
Esta lista de problemas no resueltos no es un monumento al fracaso humano; es un mapa de nuestro apetito por el conocimiento.
No se trata del millón de dólares. Se trata de que, como especie, no podemos evitar asomarnos a la oscuridad y tratar de encender una luz. Estos problemas son los límites actuales de nuestra lógica. Resolver uno no solo nos da una respuesta; nos da herramientas de pensamiento completamente nuevas que impulsarán la ciencia y la tecnología de formas que ni siquiera podemos predecir.
Oswaldo Karam lo resumió quizás de la mejor manera al final de nuestra conversación: «Es el instinto humano básico. Vemos una montaña y queremos escalarla. Vemos una puerta cerrada y queremos saber qué hay detrás. Estos problemas son las puertas cerradas más difíciles que la humanidad ha encontrado».
Referencias
URL: https://www.claymath.org/millennium-problems
URL: https://www.quantamagazine.org/the-riemann-hypothesis-explained-20210810/
URL: https://www.wired.com/2014/10/p-vs-np-biggest-unsolved-problem-computer-science/




